ユークリッド幾何学とは？5つの公理から非ユークリッド幾何学まで？ユークリッド幾何学の基礎から非ユークリッド幾何学の出現まで
古代ギリシャで花開いたユークリッド幾何学。建築から論理的思考まで、幅広い分野を支えるその基礎は『原論』の5つの公理にあります。平行線の定義を巡る論争、非ユークリッド幾何学の登場は、数学の新たな地平を切り開きました。幾何学の多様な発展と、現代科学への影響を、わかりやすく解説します。空間を理解する普遍的なツールとしての幾何学の進化を追います。
💡 ユークリッド幾何学は、建築や工学など様々な分野の基礎であり、論理的思考の土台を築きます。
💡 平面図形を学ぶ目的は、立体（3次元）の理解と論理的思考力の育成、そして社会への応用です。
💡 非ユークリッド幾何学は、ユークリッド幾何学の絶対性に疑問を投げかけ、数学に大きな変革をもたらしました。
本日はユークリッド幾何学をテーマに、その基本原則から発展、そして現代数学へのつながり、非ユークリッド幾何学までを掘り下げていきます。
ユークリッド幾何学の誕生と基本原則
ユークリッド幾何学の基礎、『原論』の公理とは？
推移律、合同、平行線など5つ。
皆さん、ユークリッド幾何学と聞くと、どのようなイメージでしょうか。
紀元前の時代に体系化されたこの学問は、現代社会においても重要な役割を果たしています。
詳しく見ていきましょう。
デジタル大辞泉における「ユークリッド幾何学」の意味、読み、例文、類語に関する情報を提供する。
さらに読む ⇒コトバンク 辞書・百科事典・各種データベースを一度に検索 出典/画像元: https://kotobank.jp/word/%E3%82%86%E3%83%BC%E3%81%8F%E3%82%8A%E3%81%A4%E3%81%A9%E5%B9%BE%E4%BD%95%E5%AD%A6-3174110デジタル大辞泉によると、ユークリッド幾何学は建築や工学の基礎になっているんですね。
5つの公理から導き出される論理の体系は、今も変わらず重要ということですね。
紀元前300年頃、ユークリッドによって体系化されたユークリッド幾何学は、建築や工学をはじめとする様々な分野で利用されています。
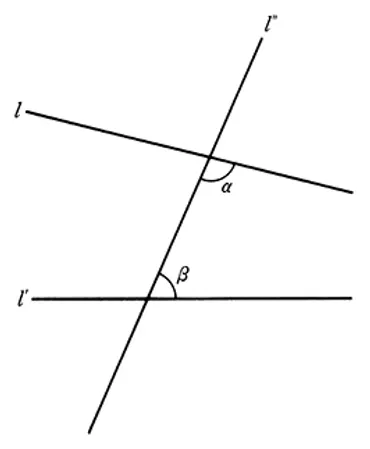
その基礎となるのは、ユークリッドが著した『原論』の中で提示された5つの公理です。
これらは、推移律、加法と減法の等式、図形の合同、全体が部分よりも大きいこと、そして平行線に関する公理を含み、論理的思考の基礎を築きました。
平面図形と5つの公理
ユークリッド幾何学で平面図形を学ぶ目的は？
応用と論理的思考力の育成！
次に、平面図形と5つの公理について見ていきましょう。
ユークリッド幾何学における平面図形とは、どのようなものでしょうか。
そして、その基本となる5つの公理とは何でしょうか。
公開日:2022/12/30
平面図形を学ぶ目的は、立体（3次元）の理解、論理的思考力の習得のため。
さらに読む ⇒学問の摩天楼出典/画像元: https://skyscraper-of-studies.com/axiom/平面図形を学ぶ目的は、論理的思考力の育成、建築や測量への応用ですか。
日常で役立つ場面を想像すると、さらに興味が湧きますね。
5つの公理は、どんなものか気になります。
ユークリッド幾何学は平面や立体の性質を扱い、その中で平面図形を学ぶ目的は、建築や測量への応用、そして論理的思考力の育成にあります。
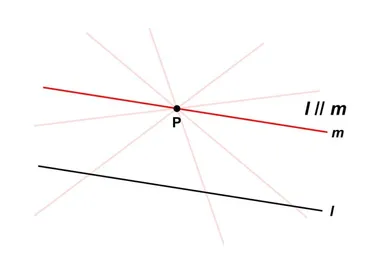
平面図形のルールとなる5つの公理は、異なる2点を通る直線を引ける、直線を無限に伸ばせる、すべての直角は等しい、任意の中心と半径で円を描ける、そして平行線の公理です。
これらの公理を出発点として、様々な定理が導き出されます。
平行線公理の探求と問題点
平行線公理、なぜ論争に？その核心は？
導けるか否かの複雑さ、それが核心。
続いて、平行線公理の探求と問題点についてです。
ユークリッド幾何学における最も論争を呼んだ、平行線に関する公理について、詳しく見ていきましょう。
公開日:2023/01/22
中学数学の図形の授業で扱う「図形の性質の証明」は、古代からある手法であり、ユークリッド幾何学として体系化されたが、中学生向けには一部を定理として扱わず、教育上の配慮から省略されている。
さらに読む ⇒大阪・上本町・高槻・西宮北口で医学部/難関大学受験を指導する個別指導塾です｜個別指導のアプロット出典/画像元: https://kobetsujuku.co.jp/column/ks191124/平行線公理が、長い間未解決問題だったとは驚きです。
その複雑さから、様々な試みがあったんですね。
どのようにして解決されたのか、興味深いです。
特に論争を呼んだのが、ユークリッドの第5公準、すなわち平行線公理です。
この公準は、直線とその直交線を定義し、交わらないという概念を示しています。
しかし、この公準の複雑さから、他の公理から導けるのではないかという試みが長年行われました。
非ユークリッド幾何学の出現と平行線の再考
平行線の定義に矛盾？非ユークリッド幾何学とは何？
ユークリッド幾何学の平行線公理に疑問を呈した学問。
非ユークリッド幾何学の出現と平行線の再考についてです。
「笑わない数学」でも取り上げられたテーマですね。
ユークリッド幾何学の常識を覆す、非ユークリッド幾何学の世界を探求しましょう。
パンサー尾形貴弘が数学の難問を解説する番組「笑わない数学」で、「非ユークリッド幾何学」をテーマにした回が放送された。
さらに読む ⇒NHK ONE出典/画像元: https://www.web.nhk/tv/pl/series-tep-Y5R676NK92/ep/MYP9GPLV4R非ユークリッド幾何学の登場で、平行線の定義に矛盾が生じたというのは衝撃的ですね。
数学の概念が、時代とともに変化していくことに驚きを感じます。
平行線の定義（交わらない二直線）は、非ユークリッド幾何学の登場により矛盾が指摘されました。
非ユークリッド幾何学では、平行線が交わることもあり、ユークリッド幾何学の平行線公理の普遍性に疑問が呈されることになりました。
平行線の証明においては、傾きの比較や同じ角度を持つという主張は誤りであり、正しい証明方法としては、定義に基づき仮定の矛盾を導くか、平行線の性質を利用して同角の仮定の矛盾を示す方法が挙げられます。
幾何学は、古典幾何学、現代幾何学、応用分野に大別され、非ユークリッド幾何学の誕生は数学の視野を大きく広げました。
幾何学の発展と未来
幾何学、どこから始まり、現代にどう影響？
古代から発展し、相対性理論など多分野に応用。
最後に、幾何学の発展と未来についてです。
非ユークリッド幾何学が、現代の数学に与えた影響、そして幾何学の今後の展望について見ていきましょう。
本書は、非ユークリッド幾何学をはじめとする現代幾何学の世界を、専門知識のない読者にもわかりやすく解説した入門書です。
さらに読む ⇒セブンネットショッピング｜本・雑誌・CD・DVD 通販出典/画像元: https://7net.omni7.jp/detail/1106783465幾何学が、古代から現代まで、様々な分野で発展してきたことに感銘を受けました。
アインシュタインの相対性理論にも繋がっているとは、本当に奥深いですね。
幾何学は、古代エジプトやギリシャで始まり、ユークリッドの『原論』によって体系化されました。
ルネサンス期には遠近法などの応用が進み、デカルトによる解析幾何学の誕生、19世紀には非ユークリッド幾何学やリーマン幾何学の確立、クラインのエルランゲン・プログラムによる幾何学の統一的分類が行われました。
20世紀以降は、アインシュタインの一般相対性理論への応用、位相幾何学や代数幾何学の発展、計算幾何学などの応用が進み、他分野との相互作用により進化を続けています。
非ユークリッド幾何学は、アインシュタインの相対性理論にも不可欠なものとなり、ユークリッド幾何学だけが唯一の正しい理論ではないことを示しました。
幾何学は、空間構造を通じて現象を理解するための道具として多様な分野に広がり、その発展は今後も続くと考えられます。
本日は、ユークリッド幾何学から非ユークリッド幾何学まで、幅広くご紹介しました。
幾何学の奥深さを改めて感じ、今後もその発展に期待したいと思いました。
💡 ユークリッド幾何学は、論理的思考の基礎であり、様々な分野に応用されています。
💡 非ユークリッド幾何学の出現は、数学の新たな可能性を示しました。
💡 幾何学は、今後も様々な分野との相互作用により発展を続けるでしょう。
