ユークリッド幾何学とは?5つの公理から非ユークリッド幾何学まで?ユークリッド幾何学の基礎から非ユークリッド幾何学の出現まで
古代ギリシャで花開いたユークリッド幾何学。建築から論理的思考まで、幅広い分野を支えるその基礎は『原論』の5つの公理にあります。平行線の定義を巡る論争、非ユークリッド幾何学の登場は、数学の新たな地平を切り開きました。幾何学の多様な発展と、現代科学への影響を、わかりやすく解説します。空間を理解する普遍的なツールとしての幾何学の進化を追います。
平行線公理の探求と問題点
平行線公理、なぜ論争に?その核心は?
導けるか否かの複雑さ、それが核心。
続いて、平行線公理の探求と問題点についてです。
ユークリッド幾何学における最も論争を呼んだ、平行線に関する公理について、詳しく見ていきましょう。
公開日:2023/01/22
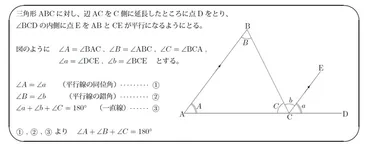
✅ 中学数学の図形の授業で扱う「図形の性質の証明」は、古代からある手法であり、ユークリッド幾何学として体系化されたが、中学生向けには一部を定理として扱わず、教育上の配慮から省略されている。
✅ 「平行線の同位角は等しい」などの定理の証明は、循環論法に陥りやすい問題があり、ユークリッドの第5公準(平行線公準)がその根幹をなす。この公準は他の公理からは証明不可能であることが長い間未解決問題だった。
✅ 19世紀に、ロバチェフスキーとボーヤイが曲面上の図形を考察することで、ユークリッドの第5公準が証明できないことを証明し、数学上の未解決問題を解決した。
さらに読む ⇒大阪・上本町・高槻・西宮北口で医学部/難関大学受験を指導する個別指導塾です|個別指導のアプロット出典/画像元: https://kobetsujuku.co.jp/column/ks191124/平行線公理が、長い間未解決問題だったとは驚きです。
その複雑さから、様々な試みがあったんですね。
どのようにして解決されたのか、興味深いです。
特に論争を呼んだのが、ユークリッドの第5公準、すなわち平行線公理です。
この公準は、直線とその直交線を定義し、交わらないという概念を示しています。
しかし、この公準の複雑さから、他の公理から導けるのではないかという試みが長年行われました。
平行線公理が未解決問題だったなんて、数学って奥深いですね!ロバチェフスキーとかボーヤイとか、名前もかっこいい!どんな発想で解決したのか、すごく知りたいです!
非ユークリッド幾何学の出現と平行線の再考
平行線の定義に矛盾?非ユークリッド幾何学とは何?
ユークリッド幾何学の平行線公理に疑問を呈した学問。
非ユークリッド幾何学の出現と平行線の再考についてです。
「笑わない数学」でも取り上げられたテーマですね。
ユークリッド幾何学の常識を覆す、非ユークリッド幾何学の世界を探求しましょう。
✅ パンサー尾形貴弘が数学の難問を解説する番組「笑わない数学」で、「非ユークリッド幾何学」をテーマにした回が放送された。
✅ 古代ギリシャ時代に確立されたユークリッド幾何学が、19世紀にその絶対性への疑問が呈され、天才数学者たちの奇妙な空想によって数学に大変革がもたらされた。
✅ 番組では、学校では教わらない「非ユークリッド幾何学」のドラマに迫り、過去の放送回や今後の放送予定についても触れている。
さらに読む ⇒NHK ONE出典/画像元: https://www.web.nhk/tv/pl/series-tep-Y5R676NK92/ep/MYP9GPLV4R非ユークリッド幾何学の登場で、平行線の定義に矛盾が生じたというのは衝撃的ですね。
数学の概念が、時代とともに変化していくことに驚きを感じます。
平行線の定義(交わらない二直線)は、非ユークリッド幾何学の登場により矛盾が指摘されました。
非ユークリッド幾何学では、平行線が交わることもあり、ユークリッド幾何学の平行線公理の普遍性に疑問が呈されることになりました。
平行線の証明においては、傾きの比較や同じ角度を持つという主張は誤りであり、正しい証明方法としては、定義に基づき仮定の矛盾を導くか、平行線の性質を利用して同角の仮定の矛盾を示す方法が挙げられます。
幾何学は、古典幾何学、現代幾何学、応用分野に大別され、非ユークリッド幾何学の誕生は数学の視野を大きく広げました。
え、平行線が交わることもあるんですか!? 概念が覆されるって、なんだかすごく面白い!もっと色々な幾何学の世界を見てみたい!発想の転換って、大事ですね!
幾何学の発展と未来
幾何学、どこから始まり、現代にどう影響?
古代から発展し、相対性理論など多分野に応用。
最後に、幾何学の発展と未来についてです。
非ユークリッド幾何学が、現代の数学に与えた影響、そして幾何学の今後の展望について見ていきましょう。

✅ 本書は、非ユークリッド幾何学をはじめとする現代幾何学の世界を、専門知識のない読者にもわかりやすく解説した入門書です。
✅ アインシュタインの相対性理論の基盤となった曲がった空間の概念や、曲面の位相、曲がり方などを、図解を交えながら丁寧に説明しています。
✅ 著者は数学者である宮岡礼子氏で、ブルーバックスシリーズの一冊として、2017年7月に講談社から発売されました。
さらに読む ⇒セブンネットショッピング|本・雑誌・CD・DVD 通販出典/画像元: https://7net.omni7.jp/detail/1106783465幾何学が、古代から現代まで、様々な分野で発展してきたことに感銘を受けました。
アインシュタインの相対性理論にも繋がっているとは、本当に奥深いですね。
幾何学は、古代エジプトやギリシャで始まり、ユークリッドの『原論』によって体系化されました。
ルネサンス期には遠近法などの応用が進み、デカルトによる解析幾何学の誕生、19世紀には非ユークリッド幾何学やリーマン幾何学の確立、クラインのエルランゲン・プログラムによる幾何学の統一的分類が行われました。
20世紀以降は、アインシュタインの一般相対性理論への応用、位相幾何学や代数幾何学の発展、計算幾何学などの応用が進み、他分野との相互作用により進化を続けています。
非ユークリッド幾何学は、アインシュタインの相対性理論にも不可欠なものとなり、ユークリッド幾何学だけが唯一の正しい理論ではないことを示しました。
幾何学は、空間構造を通じて現象を理解するための道具として多様な分野に広がり、その発展は今後も続くと考えられます。
幾何学って、こんなに色々な分野で役に立っているんですね。アインシュタインの理論にも関係しているなんて、知的好奇心が刺激されます。もっと深く学びたいです。
本日は、ユークリッド幾何学から非ユークリッド幾何学まで、幅広くご紹介しました。
幾何学の奥深さを改めて感じ、今後もその発展に期待したいと思いました。
💡 ユークリッド幾何学は、論理的思考の基礎であり、様々な分野に応用されています。
💡 非ユークリッド幾何学の出現は、数学の新たな可能性を示しました。
💡 幾何学は、今後も様々な分野との相互作用により発展を続けるでしょう。


